Introduction

With the rise of decentralized finance (aka DeFi), traders are increasingly allured by the promises of high returns on investment. One such innovation is concentrated liquidity pools, popularized by platforms like Uniswap v3. In short, it is a more efficient way to provide liquidity for pairwise swaps compared to normal liquidity pools seen on platforms like Uniswap v2.

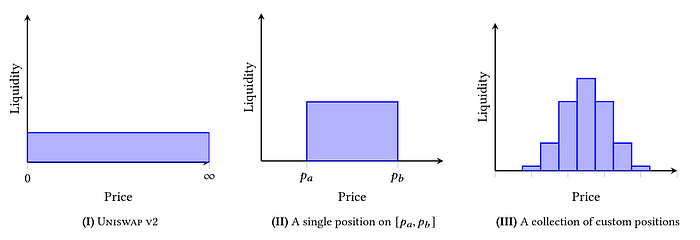
The main difference is that normal liquidity pools provide evenly distributed liquidity over all price ranges, which is less efficient as prices more or less do not fluctuate between this infinite price range. So, your capital allocation is inefficent as you are providing liquidity for prices which are not typically reached under normal market volatility. For instance, on the pair BTCUSDT, it is obviously a waste to provide liquidity at $1 or $500,000 per BTC when the trading range (as of Dec 20th, 2025) is around $90,000 +- a few thousand.

With concentrated liquidity, you as the liquidity provider (LP) can provide liquidity at specified ranges, so that your allocated capital is more efficient in normal price ranges. The narrower your range, the higher your capital efficiency is, netting you a higher percentage of swap fees in that range.

What's the catch?

The main issue with concentrated liquidity is that when your position is out of range, you may be exposed to what is known as impermanent loss as you are exposed to the price delta of whatever asset you are left holding at the end of range. Therefore, if the pair exchange never recovers to range levels, you may incur a "permanent" impermanent loss. Thus, the range must be constantly readjusted to ensure maximal capital efficiency, which also may occur losses when exiting and re-entering the pool due to the difference in asset ratios since time of initial entry, as well as fluctuations in underlying asset price. Thus, we seek to explore the viability of delta hedging the underlying assets through short positions on decentralized exchanges (DEXs).

Delta Hedging

The math behind calculating position size for a given position are detailed in this paper.

When hedging, the main factor to consider is the cost of rebalancing. When creating a position on an exchange, you are often subject to real world fees that make thin margins worse. Based on how rebalancing orders are made, you may encounter platform fees, losses related to crossing the bid/ask gap, maker/taker fees, as well as funding fees for perpetuals. The frequency of rebalancing depends on the underlying asset volatility, especially if one asset is not pegged to a specific value.

So is it useful?

A pair I've kept my eye on is S/USDC (Sonic / USD Coin). It is supported as a pair on Hyperliquid, the largest DEX, and has platforms where concentrated liquidity strategies are available, with the largest being shadow.so. Gas costs on the Sonic chain are negligible, at around $0.001 per transaction with 720ms finality.

So, in order to have a profitable delta neutral LP position, fee income must exceed all hedging costs plus residual gamma losses. With a typical volatility of 4-7% daily as exhibited on $S, rebalancings would often be many times daily.

Based on the Hyperliquid documentation, there is a 0.045% taker fee (lower for maker, but there is not guaranteed fill). Assuming multiple daily rebalancings, this would account for around 25% of the initial investment yearly. Likewise, adding on slippage, this could tack on another 40%.

With delta hedging, you are susceptible to gamma drag. Though delta hedging accounts for first order risk, the hedge position essentially buys high and sells low, leaving you with realized losses as price fluctuates. To provide an example, if S were to oscillate 2% up and down and you had a CL position in the 2% band, your CL position would sell S as price rises (converting more into USDC). As it goes out of range, your exposure to S on the CL position drops from 50% to 0%. To stay delta neutral, you must reduce your short by buying back around 50% of S at this higher value. As the price falls back down to the original, your S exposure increases from 0% to 50% on the CL position. To stay delta neutral, you now must increase your short position by selling 50% of S at the lower value. So, overall, you would have bought $x at +2%, then sold that same amount at 0%, leaving you with a 2% loss on the exposure amount, or 1% of your hedge overall.

Though the CL position remained unchanged, your hedge lost 1% of its value during this volatility swing. If this happens even once a day (conservatively), 1% a day * 365 creates 365% of the initial position in gamma drag.

So, you would need to sustain an average APR of 400% (or much more, depending on actual volatility) to make a profit in the best case. Currently, the 2% band on Shadow lists an APR of 1096% but it would have to average out over this amount over a long time frame to see return on investment.

Conclusion

Maybe it works? We will find out in the next blog post. Or when I go broke. Cheers!